1.8 Función exponencial y logaritmica

1.8 Función exponencial y logarítmica

La función exponencial es de la forma y=ax , siendo a un número real positivo.

Se llama función exponencial a aquella cuya expresión es: f ( x ) = k . ax + b Esta función tiene por dominio de definición el conjunto de los números reales, y cuenta con una característica particular, ya que su derivada es la misma función.

En la expresión f ( x ) = k . ax + b, el número k es real y distinto de cero, mientras que a es un número real positivo y distin¬to de uno.

Entonces:
• El número k es distinto de cero, ya que si no fuera así, quedaría una función constante: f ( x ) = b , porque se anula el primer término.

• El número a, por su parte, debe ser mayor que cero, ya que si a fuera un número negativo, por ejemplo -4, no podríamos elevarlo 1/2, es decir, sacar su raíz cuadrada. 

En el gráfico, la función es creciente, ya que a es mayor que uno, corta al eje de las ordenadas en uno y no tiene raíces, no corta al eje x.

A medida que los valores de x son menores, y toma valores cada vez más próximos a cero. En ese caso, decimos que la función tiene una asíntota horizontal en y = 0. 

El dominio de la función son todos los números reales mientras que la imagen son los números reales mayores que cero.

Función logarítmica:

La función logarítmica es del tipo f ( x ) = logb x donde b representa a un número real dis¬tinto de 1 y x es siempre mayor que 0 b ? R; b = 1; x > 0 .

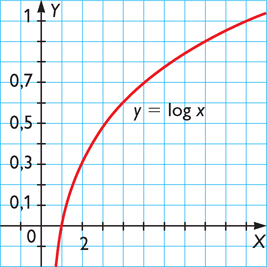
La gráfica de la función logarítmica f ( x ) = log2 x es: 

Es una gráfica que no corta al eje y, a meddida que x toma valores cada vez más próximos al 0, y toma valores cada vez menores. La gráfica muestra que la función es creciente, y corta al eje x en 1 porque todo número distinto de 0 elevado a la 0 da por resultado 1. Por lo tanto, en la función logarítmica la asíntota es vertical.