1.5 Composición de funciones.

  1.5  Composición de funciones.

Dadas dos funciones reales de variable real, f y g, se llama composición de las

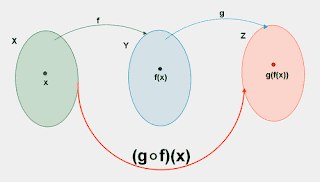
funciones f y g, y se escribe g o f, a la función definida de R en R, por (g o f )(x) = g[f(x)].

La función ( g o f )(x) se lee « f compuesto con g aplicado a x ».

 

 

Primero actúa la función f y después actúa la función g, sobre f(x).

Cálculo de la imagen de un elemento mediante una función compuesta

Para obtener la imagen de la función compuesta aplicada a un número x, se siguen estos pasos:

1. Se calcula la imagen de x mediante la función f, f(x).

2. Se calcula la imagen mediante la función g, de f(x). Es decir, se aplica la función g al resultado obtenido anteriormente.

Ejercicio:

 Sean las funciones f(x) = x + 3 y g(x) = x².

Calcular g o f y la imagen mediante esta función de 1, 0 y -3.

Resolución:

 

       

· La imagen de dos números 1, 0, -3, mediante la función g o f es:

‚ Dadas las funciones f(x) = x² + 1, y g(x) = 3x - 2, calcular:

a) (g o f ) (x)

b) (f o g ) (x)

c) (g o f ) (1) y (f o g ) (-1)

d ) El original de 49 para la función g o f.

Resolución:

 

 

                                                                      

 

 

                                                                        

c) Aplicando los resultados de los apartados anteriores:

(g o f ) (x) = 3x² + 1 = 49. Basta con resolver esta ecuación.